TUJUAN
1. Memahami prinsip kerja tabulasi/ Quine Mc-Cluskey
2. Mendesain rangkaian dari penyederhanaan dengan tabulasi Quine Mc-Cluskey
DASAR TEORI
Metode tabulasi dapat mengatasi fungsi yang kompleks, dimana memiliki variabelyang banyak. Metode tabulasi terdiri atas dua bagian;
1.Menemukan kandidat-kandidat dari fungsi Boolean yang diberikan untuk fungsi penyederhanaan, atau disebut juga prime implicant
2.Memilih diantara prime implicant tersebut yang paling minimal dalam meng-cover fungsi Boolean.
Langkah-langkah untuk menentukan prime implicant :
1.Membuat daftar minterm-minterm dari fungsi Boolean
2.Mengubah setiap meinterm ke dalam bentuk biner
3.Susun setiap minterm binary dalam bentuk kelompok-kelompok, dimana dalamsatu kelompok harus memiliki jumlah angka satu yang sama.
4.Lakukan Matching process, yaitu mengkombinasi minterm-minterm antara grup yang bersebelahan. Minterm-minterm yang dapat dikombinasi adalah minterm yangmemiliki perbedaan satu variabel saja pada minterm binary atau dalam hitungandecimal memiliki selisih 2n. Perbedaan satu variabel tersebut kemudian digantidengan dash (-).
5. Tandai dengan (√) bila minterm tersebut telah dikombinasi dengan minterm padakelompok yang bersebelahan.
6. Matching process diulangi terus hingga tidak lagi minterm-mintern yang tidak bisakombinasi.
7.Kombinasi-kombinasi minterm yang tidak ditandai dengan (√) menjadi kandidat prime implicant .
Sebuah fungsi Boolean F(A,B,C,D) = Σm( 0 , 2 , 4 , 6 , 7 , 8 , 10 , 11 , 12 , 13 , 14 , 16 , 18 , 19 , 29 ,30 ), akan disederhanakan menggunkan metode tabulasi. Langkah-langkah sebagai berikut :
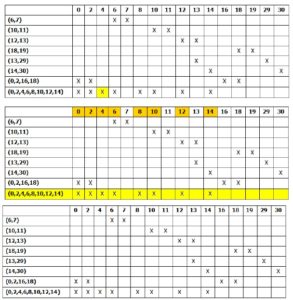
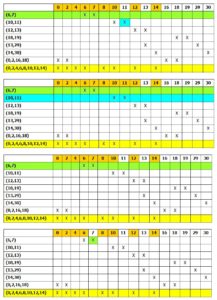
1.Membuat daftar minterm-minterm dari fungsi Boolean. Mengubah setiap minterm kedalam bentuk binary. Menyusun setiap minterm binary dalam bentuk kelompok –kelompok, dimana dalam satu kelompok harus memiliki jumlah angka satu yang sama.

2.Lakukan Matching process, yaitu mengkombinasi minterm-minterm antara grup yang bersebelahan. Minterm-minterm yang dapat dikombinasi adalah minterm yang memiliki perbedaan satu variabel saja pada minterm binary atau dalam hitungan decimal memiliki selisih 2n.. Perbedaan satu variabel tersebut kemudian diganti dengan dash (-).

Tandai dengan (√) bila minterm tersebut telah dikombinasi dengan minterm pada
kelompok yang bersebelahan.
3. Matching process diulangi terus hingga tidak lagi ditemui minterm-mintern yang tidak bisa kombinasi.

4.Kombinasi-kombinasi minterm yang tidak ditandai dengan (√) menjadi kandidat prime-implicant.

Selanjutnya berikut langkah-langkah untuk memilih diantara prime implicant yang paling minimal dalam meng-cover fungsi Boolean, yaitu :
1.Buat tabel Prime implicant , dimana X-axis adalah minterm dan Y-axis adalah primeimplicant . Tandai dengan (x), pada pertemuan antara baris dan kolom yang menunjukkankomposisi dari minterm-minterm yang menyusun prime implicant.
2.Pilih prime implicant yang essential pada baris, dimana baris tersebut meng-cover (x)yang hanya ada satu secara vertikal. Tandai semua prime implicant yang essential.
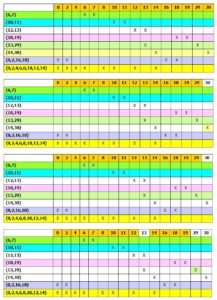
3. Susun fungsi SOP dengan prime implicant yang telah terpilih.
F( A,B,C,D,E) = ∑m(0,2,4,6,7,8,11,12,13,14,16,18,19,29,30)
= (6,7)+ (10,11)+ (18,19)+ (13,29)+(14,30)+(0,2,16,18) +(0,2,4,6,8,10,12,14)
= A’B’CD+ A’BCD + AB’CD +BCD’E + BCDE’ + B’CE’ + A’E’Metode Patrick merupakan metode untuk mengatasi kelemahan dari metode tabulasi apabila pada tahap kedua (Pilih prime implicant yang essential) tidak dapat meng-cover semua minterm. Pada contoh di bab metode tabulasi, semua minterm Σm
(0,2,4,6,7,8,10,11,12,13,14,16,18,19,29,30) telah dapat di-cover oleh fungsi:
F( A,B,C,D,E) = A’B’CD+ A’BCD + AB’CD +BCD’E + BCDE’ + B’CE’ + A’E’
F( A,B,C,D,E) = ∑m(0,2,4,6,7,8,11,12,13,14,16,18,19,29,30)
= (6,7)+ (10,11)+ (18,19)+ (13,29)+(14,30)+(0,2,16,18) +(0,2,4,6,8,10,12,14)
= A’B’CD+ A’BCD + AB’CD +BCD’E + BCDE’ + B’CE’ + A’E’Metode Patrick merupakan metode untuk mengatasi kelemahan dari metode tabulasi apabila pada tahap kedua (Pilih prime implicant yang essential) tidak dapat meng-cover semua minterm. Pada contoh di bab metode tabulasi, semua minterm Σm
(0,2,4,6,7,8,10,11,12,13,14,16,18,19,29,30) telah dapat di-cover oleh fungsi:
F( A,B,C,D,E) = A’B’CD+ A’BCD + AB’CD +BCD’E + BCDE’ + B’CE’ + A’E’
Selain itu dapat dilihat pada tabel terakhir metode tabulasi, semua kotak pada baris pertama telah diberi warna kuning semua, yang berarti semua minterm telah di-cover. Bagaimana bila tabel terakhir yang diporeleh dari metode tebulasi seperti yang ditunjukkan pada tabel.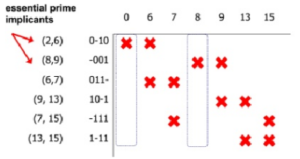
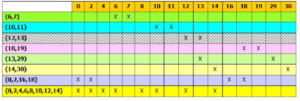
Fungsi akhir, hasil metode tabulasi adalah F = wʹ.y.zʹ + xʹ.yʹ.z Dimana ada beberapa minterm yang belum ter-cover , seperti yang ditunjukan pada Gambar
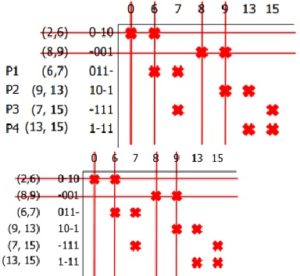
Minterm-minterm yang belum ter-cover adalah Σm(7,13,15). Prime implicant yang meng-cover minterm-minterm tersbut adalah (6,7), (9,13), (7,15), dan (13,15).Bagaimana cara memilih diantara prime implicant tersebut yang dapat meng-cover semuaminterm. Maka dibutuhkan metode Patrick untuk mengatasi masalah tersebut.Langka-langkah metode patrik untuk menentukan peng-cover-an yang paling minimal adalah :
1.Beri label pada baris prime implicant yang memiliki minterm yang belum ter cover , misalnya P1, P2, P3, P4.
2.Tentukan persamaan logical dalam bentuk POS, dimana pada masing-masing summemiliki minimal satu minterm yang sama.
P = (P1 + P3)(P2 + P4)(P3 + P4)
3. Ubah bentuk POS ke bentuk SOP,dengan cara mengalikan. Beberapa aturan yang perlu diingat :
a. X + XY = X
b.X.X = X
c. X.Y.X = X.Y
Maka Persamaan bentuk SOP–nya adalah :
P = (P1 + P3)(P2 + P4)(P3 + P4)
P = (P1 + P3)(P2P3 +P2P4 +P4P3 + P4P4)
P = (P1 + P3)(P2P3 +P2P4 +P4P3 + P4)
P = (P1 + P3)(P2P3 +P2P4 +P4)
P = (P1 + P3)(P2P3 + P4)
P = P1P2P3 + P1P4 + P3P2P3 + P3P4
P = P1P2P3 + P1P4 + P2P3 + P3P45.
Masing-masing bentuk minterm pada SOP merupakan reprentasi dari solusi yang dapatmeng-cover sisa minterm pada tabel … di langkah pertama. Pilih minterm yang memiliki jumlah variabel sedikit, yaitu P1P4 , P2P3, P3P4.Sehingga ada 3 pilihan prime implicant :
a. P1P4 = wʹxy ,wyz
b. P2P3 = wxʹz , xyz
c. P3P4 = xyz , wyz6.
Fungsi finalnya = prime implicantessential + salah satu solusi prime imlicant.
Misal dipilih solusi ketiga (c) , sehingga persamaan minimalnya:
F = wʹ.y.zʹ + xʹ.yʹ.z + x.y.z +w.y.z
sumber:
Modul Matakuliah Elektronika Digital

0 Responses
Stay in touch with the conversation, subscribe to the RSS feed for comments on this post.